View the Earth as ℂℙ¹ and let f: [0,1] → ℂℙ¹ be your path and choose p, q ∈ ℂℙ¹(im(f) ∪ {∞}) as before. Let n_p and n_q be the winding numbers around ∞ wrto stereographic projection from p, q respectively.
I am going to add an additional restriction that p and q aren’t antipodal, but I think this is reasonable since CP1 is Hausdorff and it shouldn’t change things if f is a tame curve. Main reason to do this is so that there’s a unique shortest geodesic from p to q, let this be g.
Imagine travelling along g from p to q counting the intersections with f with sign. For every intersection where f crosses your path left-to-right, count the intersection as +1, for every intersection where g crosses right-to-left, count it as -1. Let the total be g∩f, then n_q = n_p + g∩f.
The proof is kinda faffy, but the essential idea is to think about a Möbius transformation which preserves the location of ∞ and f(1), but maps p to q.
If f doesn’t cross g, this map doesn’t change the winding number. If f crosses g once from left-to-right as seen from g, this increases the winding number by 1. The RTL sign is determined by homotopy.
EDIT: I found a few sign errors and slip-ups, but the proof below should be correct.
It is technically easier to assume that the north pole is at 0, and we are instead projecting away from either p or q. We use this scheme going forward.
Given signed curves γ, η: [0,1] → ℂℙ¹, define their intersection number, γ∩η, as follows: - let γ∩η = 0, - travel along γ, - if η intersects γ right-to-left, add 1 to γ∩η, - if η intersects γ left-to-right, add -1 to γ∩η.
Moreover, if γ(1) = η(0), we define their concatenation, η*γ, to be the map: (η*γ)(t) = γ(2t) if t ≤ 0.5 else η(2t - 1).
One can show that if λ is a third curve we have, (η*γ)∩λ = η∩λ + γ∩λ.
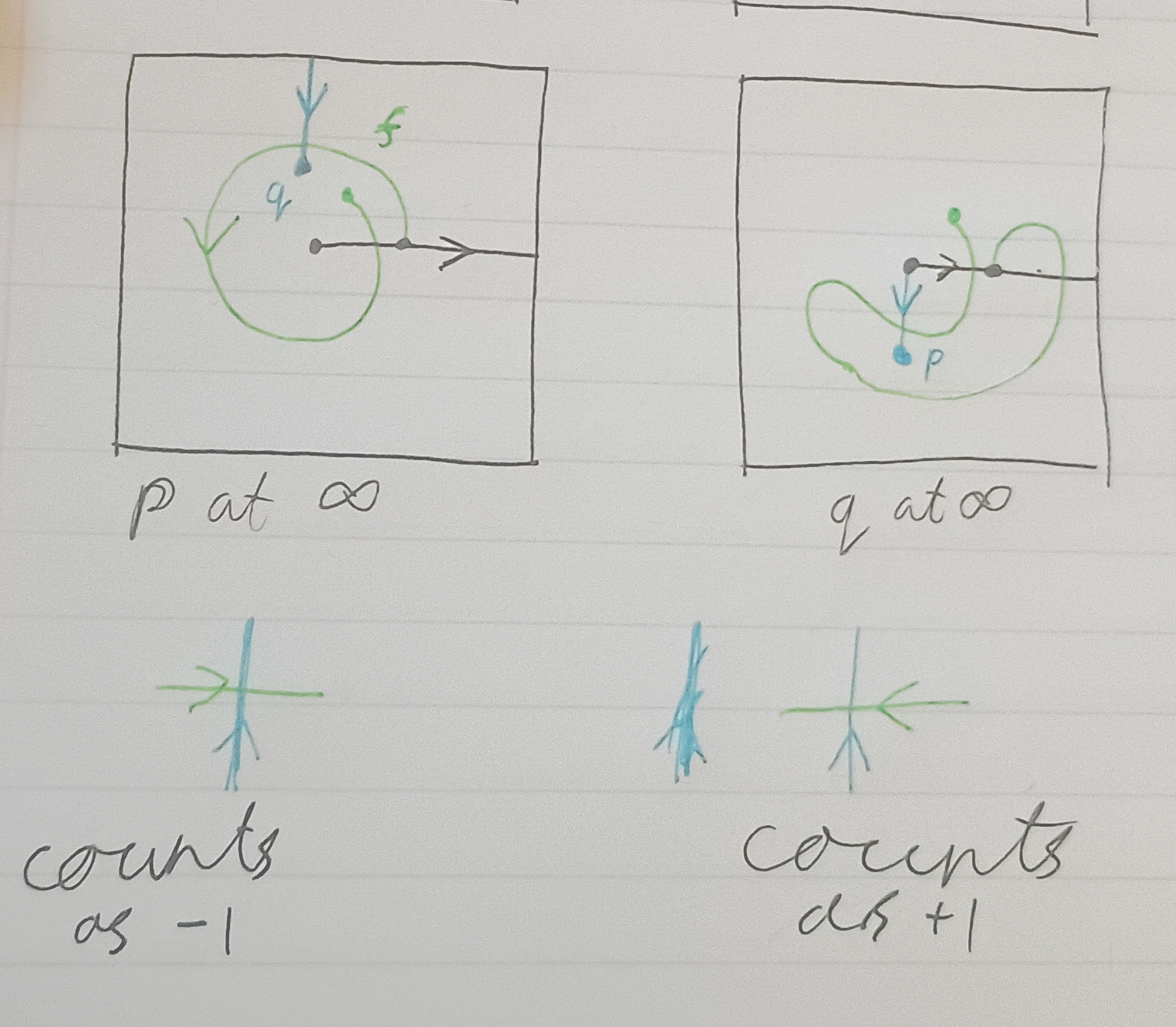
Now consider the setup below.

WLOG, assume that f(0) = 1 and recall that in this scheme the north pole is at 0. When p is at ∞, let R_p be the ray from 0 to 1 (drawn in black in the image below). Note that as a map into ℂℙ¹, this terminates at p. The winding number is then the intersection number R_p ∩ f.
Now when q is at infinity, we let R_q be the ray from 0 to 1 which terminates at q. We can view R_q as the concatenation of R_p and an arc from p to q, R_{pq} say. It then follows that:
n_q = R_q∩f = (R_{pq}*R_p)∩f = R_{pq}∩f + n_p.
And we are done.